https://arxiv.org/pdf/2310.15213
모델이 어떻게 ICL(in-context learning)을 하는가?

Related works
ICL (In-context learning)
언어모델이 inference time에 적은 수의 demonstration에서 어떤 task를 푸는것인지 '학습'하는 것
1. transformers are few shot learner; GPT3 논문에서 처음으로 제시됨
2. https://arxiv.org/abs/2211.15661 에서 ICL이 synthetic task (linear regression)에서 Stochastic Gradient Descent임을 간접적으로 보임
3. https://arxiv.org/pdf/2212.10559 에서 ICL이 일반적인 NLP task에서 gradient descent로 learning하고 있음을 보임. 특히 수학적으로 어텐션이 gradient descent를 근사할 수 있음을 보임.
4. https://arxiv.org/pdf/2111.02080 에서 ICL을 Bayesian Inference로 해석해서 어떤 조건에서 ICL이 일어나는지 수학적으로 보임.
5. https://transformer-circuits.pub/2022/in-context-learning-and-induction-heads/ induction head가 ICL을 수행하는 주요 메카니즘임을 간접적으로 보임
Task Vector
https://arxiv.org/pdf/2212.04089 에서 특정 task에 finetuning된 모델과 기존모델의 weight의 차를 human intuition에 맞게 vector arithmatic이 가능한 벡터임을 보임

Contribution
1. ICL task를 푸는 mechanism으로 function vector를 제시함
2. function vector를 unembedding해서 해석함
3. function vector도 위 task vector처럼 human intuition에 맞게 vector arithmatic이 가능함을 보임. 특히 compositional task를 수행 할 수 있음을 보임
Method
Intuition

model steering (representation engineering) 하듯이 (a) ICL 프롬프트 마지막 포지션 특정 레이어 l의 residual stream의 평균벡터 h를 구하고, zero shot setting의 (b)에서 inference time에 h를 추출했던 레이어, 프롬프트 마지막 포지션에 h를 더하면 최대 24.3%의 accuracy로 반의어 task를 풀었다. (12번레이어 에서 최대)
Function Vector
위 방법을 좀더 fine grained 하게 해서 최적의 벡터 (위에서 h)를 찾고싶다.
Setup
1. P : task별 데이터셋; p = [(xi1, yi1), ... (xiN,yiN), xiq]; task별로 각 프롬프트에 N개의 ICL 토큰쌍이 주어지고 모델이 예측할 토큰이 yiq 가 되는 xiq가 주어진다. (예를 들어 위와 같이 antonym task면 단어:반의어 쌍)
2. P (논문에서 tilede p) : 위와 마찬가지로 p = [(xi1, yi1), ... (xiN,yiN), xiq] 형태의 데이터셋이지만, yi 가 각 쌍에 대해 shuffle되어 있다. 사실상 형태는 P와 동일하되 in context에서 learn할게 없는 형태
(실제 실험에서는 task당 100개의 10shot prompt를 이용함)

(프롬프트 형태는 위와같음)
Attention contribution patching
어느 레이어, 어텐션헤드의 contribution이 중요한지 찾겠다.

특정 task t에 대해 Pt에서 특정 l레이어 j번 헤드의 모든 프롬프트에서 마지막 포지션 contribution 벡터의 평균을 구한다.
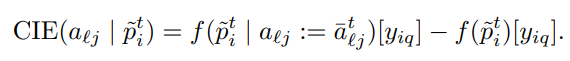
프롬프트 p (context 가 shuffle된 프롬프트)를 넣은 inference time에 마지막 토큰 포지션(':' 포지션) 의 attention contribution 벡터를 위에서 구한 평균벡터로 대체했을때와 대체하지 않고 그냥 inference했을때 실제 정답토큰 yiq에 assign된 확률의 차이를 CIE (causal indirect effect) 로 정의

모든 task, 각 task 모든 prompt에 대해 CIE의 평균을 AIE (average indirect effect) 라 한다. 즉 (레이어,헤드) 하나당 AIE를 구할 수 있다.

위와같이 소수의 특정 레이어 특정 헤드의 contribution만 중요함을 알 수 있다. (GPT-J에서의 plot)
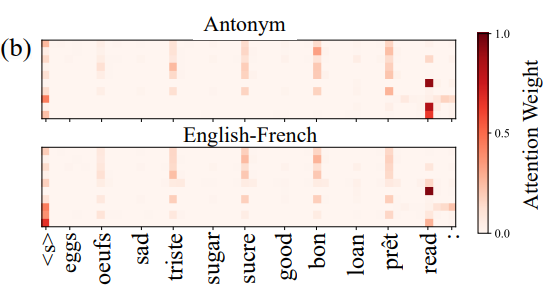
위에서 찾은 헤드들의 반의어 task, 영-프 번역 task에서 last position attention pattern task별 평균내서 plot한 결과
다음 토큰을 예측하기 위해 context상 토큰 쌍에서 2번째 토큰(y들)이 오는 위치 + 현재의 x에서 attention score가 높은것을 확인할 수 있다. (induction head에서 확인한 내용과 일치) (GPT-J에서의 plot)

위에서 찾은 주요한 contribution을 하는 head의 contribution 벡터를 task별로 평균내서 function vector로 사용한다. 모델 크기에 따라 top10부터 top100의 a를 사용한다.
이 function vector를 inference time에 마지막 포지션, 특정 레이어 residual stream에 더해줘서 in context learning을 context없이 해보겠다. (attention 의 contribution들의 평균; 즉 원래 residual stream에 더해질 벡터였다)
Experiment
Setup

실험에 사용한 모델들; 전부 GPT (decoder only) 모델. 가장 우측 al은 헤드 수

실험에 사용한 task.
Adding Function Vector

위에서 구한 function vector를 전체 레이어 중 1/3번째 레이어 마지막 포지션 residual stream에 더해주었을때,
Shuffled label에서 90.7%-96.5%의 accuracy를, Zero-shot에서 llama2의 경우 83.8%의 accuracy를 보인다.
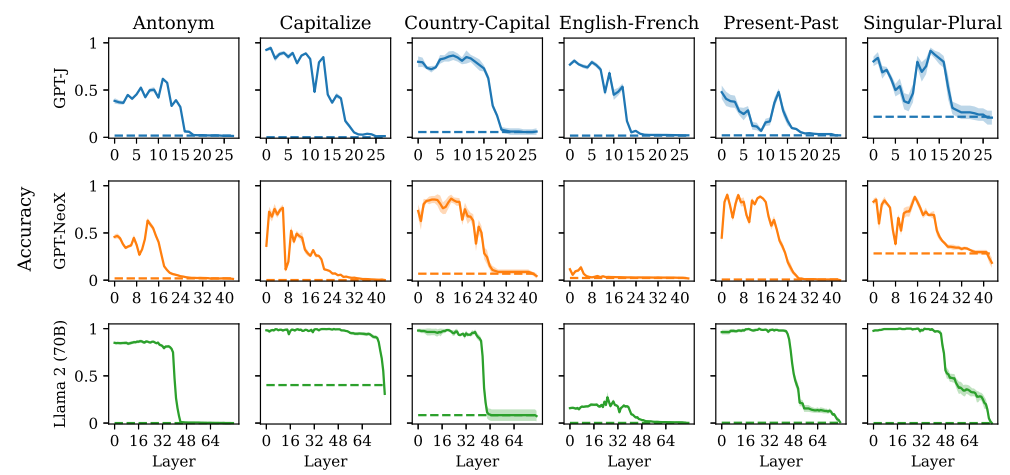
레이어별로 더했을때 task별 accuracy
즉 앞에서 찾은 function vector로 모델에게 task를 알려줄 수 있다. transferable feature
Function Vector on Different Forms
function vector를 찾을때는 x1:y1 ..." 의 형태에서 추출했다. 이제 이 function vector 일반적인 자연어 형태(autroregressive prediction)에서 어떻게 작동하는지 확인한다.

위와같이 다양한 프롬프트를 주고 프롬프트 이후 생성한 5개 토큰에 정답 토큰(위 경우에는 반의어)이 있는지 확인한다. task에 상관없이 유의미한 accuracy를 보인다.

ICL을 통해서 생기는 task의 representation이 일반적인 자연어 형태(autroregressive prediction)에서 쓰이는 representation과 유사하다고 할 수 있다.
Function Vector Projected to Vocab Space

Function vector는 attention contribution의 평균이기 때문에 residual과 사이즈가 동일하다. 이를 unembedding하여 가장 높은 확률 토큰부터 나열한 결과, 위와같이 대부분 task의 y가 될 수 있는 토큰들 (국가-도시 에서 파리, 런던 등) 이다. 그 외 반의어(Antonym)의 경우 반의어의 abstract한 의미를 갖는 토큰들이고 영-프번역(English-French)의 경우 의미없는 토큰이다.
그렇다면 의미있는 디코딩에 성공한 task들의 function vector; 특히 디코딩 했을때 y에 속하는 토큰들을 높은 확률로 예측하는 task들의 function vector를 학습해서 만들 수 있는가?

unembeding D를 고정, residual stream과 동일한 차원의 벡터 v를 실제 function vector의 unembedding과의 CE를 최소화 하도록 학습한다.

function vector의 기능 일부를 재현 가능한 것으로 보이나 실제 function vector와는 성능 차이가 크게 난다. 즉 unembed되어 interpretable하게 token으로 표현된 정보 이상의 무언가가 있다고 생각할 수 있다.
Function Vector Arithmatic
function vector는 functional behaviour라는 abstract한 공간에서 word vector arithmatic처럼 composition이 가능한가?
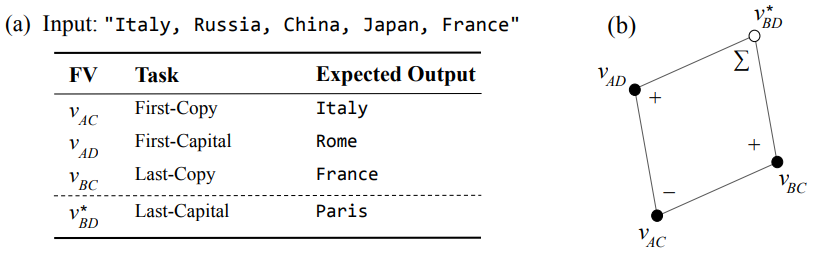
위와같이 주어진 list (Italy, Russia, China, Japan, France) 에서 마지막 토큰 (France) 의 수도를 생성하는 task는 위와같이 composition을 만들 수 있다.

이렇게 만들어낸 function vector의 task별 성능은 다음과 같다.
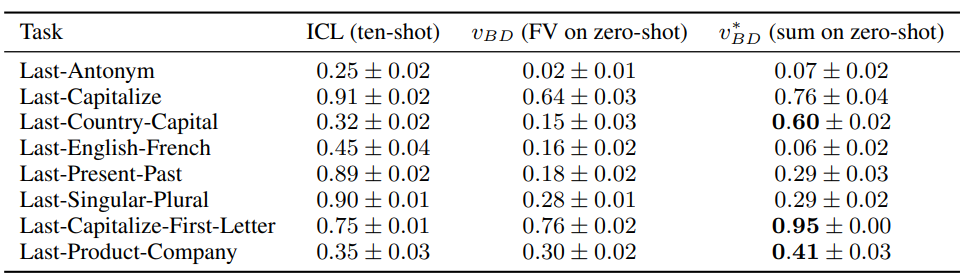
많은 경우에서 function vector와 유사한 성능을 보여주고 일부 경우에서는 ICL자체보다 우월한 성능을 보인다. 반면 일부 task에서는 ICL, function vector보다 못한 경우도 존재한다.
위와같이 task의 composition이 단순 vector arithmatic으로 가능하다는것은 모델이 실제로 "word-selection"(copy task)과 "word transformation"(to capital task)를 따로 function vector를 이용해 풀고 있다는 간접적인 증거가 된다.
Dicussion
1. Concurrent work
https://arxiv.org/pdf/2310.15916
거의 동일한 세팅의 실험을 한 paper. 본 논문과는 다르게 contribution을 더하는 대신 residual stream을 patch(교체)한다.

function vector를 patch하되 zero-shot 세팅이 아니라 아예 adversarial하게 앞의 프롬프트에 다른 task의 few shot example을 제공한다. 이때 function vector의 영향이 더 강해 function vector task에 대해 77-95%의 accuracy를 보여준다. 즉, attention의 효과보다 function vector의 영향이 더 큰 모습을 보여줌 (위에서도 말했듯이 여기서는 attention contribution을 더해준 것이 아니라 patching을 한거임)
2. followup work
https://arxiv.org/pdf/2311.06668
실질적으로 이 아이디어를 이용해서 task를 품
3. function vector arithmatic VS word vector arithmatic
word vector arithmatic에서 유명한 예시 king - man + woman = queen 에서 woman-man을 여기의 function vector와 같다고 생각하면 안된다.
function vector는 cyclic한 task도 풀 수 있다.
예를 들어 word vector스타일로 반의어를 풀어보면 : big - small 을 반의어 function vector로 사용한다고 치자. 이때 big + (big - small) = small 이 되어야 하는데 그러려면 big = small 이어야 한다... 즉 word vector arithmatic으로 이 문제를 풀 수 없지만 실제로 function vector는 이 문제를 풀 수 있었다.
이하는 해볼만한 실험들
4. funtion vector on representation?
다른 representation engineering 연구의 representation에 function vector를 적용(composition)할 수 있는가?
5. why not ablate?
function vector를 빼거나 orthogonalize하면 더이상 해당 task를 풀 수 없게 되는가?